The Mother's Curse

Summary
The Trojan Female Technique appears to be an effcient method to reduce the size of a pest population, possibly to extinction, and keep it down. Through the analysis of the continuous time model we have found that we can split the long term solutions into three groups depending on the size of the initial introduction of Trojan females:
- If the initial introduction is above the extinction boundary the population will become extinct in the long run. We have found an approximate representation of this extinction boundary, defined by a straight line parallel to the T = T* line, shifted to the right by the amount T0* — T0. Through simulation we also found that, as the birth rate l increases the size of T0* — T0 decreases relative to the population size. This suggests that proportionally fewer Trojan females are needed to bring the population to extinction. The death rate parameter µ has the opposite effect.
- If the initial introduction is below the T* = T line, the population tends towards an equilibrium that lies on an attracting manifold which we definene implicitly by
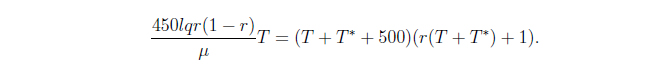
The "lower bound" and "upper bound", between which the equilibrium must lie, are defineded explicitly in terms of the parameter values used by
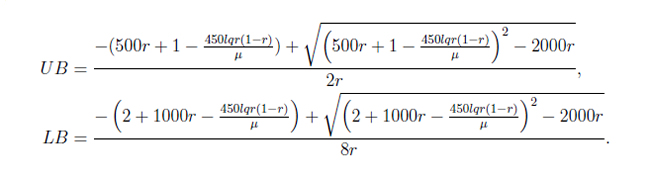
The upper bound corresponds to the equilibrium solution of the population before Trojan females are introduced and the lower bound is the point where the T* = T line crosses the attracting manifold. These equations were derived assuming that the gender proportions in the population were at equilibrium. We found that this has little effect on the long term solutions and any effect it does have will actually act in favour of extinction.
Again through simulation we found that increases in the parameters l and q cause a decrease in the distance between the two bounds relative to the population size, allowing for relatively fewer possible equilibrium points. The parameters r and µ had an opposite eect.
- If the initial introduction is between the T* = T line and the extinction boundary, we cannot be certain whether the population will go extinct or end up at an equilibrium on the attracting manifold.
We also explored the use of the Wolbachia bacteria in conjunction with the Trojan Female Technique. We found that this can aid our goal of extinction, but only if Trojan females and Wolbachia infected females, or a combination of males and females, are introduced separately. When introduced together (i.e. Trojan-Wolbachia females) the combination actually has a negative effectt on the efficacy of the TFT.
In the ongoing research on the Trojan Female Technique we wish to explore further the following areas:
- The effect of including the juvenile stage, introduced in Chapter 3, in our model. This will include looking into a different representation of the population behaviour, using only the density of adults rather than the total density.
- Analysis of the discrete and stochastic models that are attached in Appendix 1. We derived these models from the continuous time model, however have yet to carry out an in depth analysis. The effect of stochasticity on the long term solutions will be of particular interest in future work.
- Investigation into the other effects of Wolbachia and how this could be combined with our current model. So far we have only looked into the effect of cytoplasmic incompatibility (CI), however there are three other ways in which Wolbachia are known to affect the reproductive fittness of individuals and we wish to explore the application of these to the TFT.
- A spatial extension to our model. Currently the dynamics of the population only depend on time, under the assumption that we have a closed population. We wish to extend this to incorporate a spatial component to study how the migratory behaviour of pests affects the efficacy of the TFT.
