Ecological models – their form and function

Cartoon - Susan Marks.
Mention ecological modelling and many people run screaming in horror. For some, this response is due to visions of bearded ecologists working with imaginary and irrelevant data, but for most it’s because people think modelling is full of complex mathematical equations that are far too difficult to comprehend. Mandy Barron offers a different perspective and here seeks to explain and encourage their wider use.
Although equations can be daunting at first, Mandy reports that if you persevere with them, they provide a far more precise, concise and universal method of expressing a hypothesis about how an ecological system works than any long-winded verbal or written description. The first step in model development – writing it out – can be a useful exercise in itself because it forces researchers to clarify their mental model, make their assumptions explicit and to identify any knowledge gaps. Unlike their runway counterparts, i.e. fashion models, ecological models are not ornamental but are developed to understand and explain field or laboratory observations and to make predictions about how systems respond. For example, Whitehead and Tompkins determined which mode of transmission best described the epidemiology of a new disease in Tasmanian devils in order to predict its impact on devil populations.
Thus, models are an abstract description or generalisation of a system. They do not, nor should they attempt to describe allof the complexity and heterogeneity in a natural system, as by the time this is done, the need for the model would have long since passed. The mark of a good model is that it is useful, i.e. fit for the purpose intended, be that explaining patterns in data, generating testable hypotheses, or identifying pivotal processes or parameters that need more data (e.g. Jones et al. are collecting data on the breeding success of grey-faced petrel to build a population model that can then be used to assess the effects of rats on bird abundance). Modelling is an indispensable tool for ecological sciences where it is often difficult, impossible, too expensive or unethical to conduct replicated, manipulative experiments, because it allows notional experiments to be conducted or a variety of management interventions on modelled systems to be examined (e.g. Warburton models the profitability of harvesting possums for fur over a range of initial possum densities).
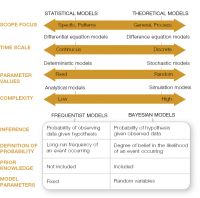
Besides the equations, another aspect that puts people off modelling is the jargon that arises from the diversity of models available (Fig.). People often draw a distinction between “statistical” or “empirical” models versus “theoretical” or “mechanistic” models. The former are fitted to data gathered as part of an experiment and are used to explain patterns and draw inference particular to that system (e.g. Gormley et al., on distribution modelling of sambar deer), while the latter use mechanistic functions to describe general ecological processes and are used for understanding and prediction.
Systems can be modelled in “continuous time”, which calculates rates of change in infinitesimally small time-steps, using differential equations, and is useful when modelling populations of species that have overlapping generations. Alternatively systems can be modelled in “discrete time”, which, as the name implies, models the state of the system at relatively large time-intervals, using difference equations, and is useful when modelling populations of species that have only one generation per annum.
Another dichotomy is between “deterministic” and “stochastic” models. For a given set of parameter values, a deterministic model will produce the same results every time whereas a stochastic model will draw the value for a model parameter from a probability distribution and thus will produce different results with each run.
“Analytical” models are usually theoretical models where the mathematical equations can be solved algebraically to understand the model’s behaviour (e.g. Holland explores the consequences of changing possum density and foraging behaviour on mortality rates of kāmahi in a herbivory model). Often models are too complex to solve directly and/or include stochasticity (random behaviour), so they can only be determined by “simulation”, which means running the model multiple times, usually over a range of parameter values, then collating and analysing the outputs (e.g. Shepherd et al. in his description of the national possum model).
There’s also a new class of model gaining popularity that promises to bridge the gap between statistical and theoretical models, but unfortunately also has its own jargon! “Bayesian” statistical models essentially involve updating “prior” or previously held beliefs in a hypothesis (formulated as a model with known or unknown parameters) in light of new observations. The updated probability is the probability of the hypothesis being true given or conditional on the observed data. For example, Nugent uses Bayesian analysis to provide managers with a posterior probability that TB has been eradicated from wildlife vectors in an area, given negative surveillance and testing results. Using a similar approach, Parkes estimates the probability that the eradication of a target pest has occurred given no further animals are found. A key difference between Bayesian inference and classical (frequentist) inference is that Bayesian analysis assumes model parameters are random values whereas frequentist analysis assumes model parameters are fixed, true quantities (Fig.). This means Bayesian analyses can accommodate uncertainty at all levels in the modelling process: in the model parameters, in the process being modelled, and in the observation of that process (e.g. Anderson) included observation error in his Bayesian analysis of pig home range use). This hierarchical approach is handy for ecological data, which often comprise piecemeal observations measured at different scales and thus don’t conform to the assumptions of frequentist statistical models.
The above has been a brief overview of common modelling terminology but in reality there are as many different model “types” as there are ecological questions. Mandy believes that there are models to fit every situation and that good science and management demand their wider use.
This work is funded by the Foundation for Research, Science and Technology (Programme C09X0909: Invasive Mammal Impacts on Biodiversity).