Incorporating uncertainty in modelling the probability of freedom of bovine tuberculosis

Eradication of disease from an area is a discrete event; it either occurs or does not (e.g. ‘heads’ in a coin toss). If we find a diseased animal, we know for certain that the eradication attempt failed. Unfortunately, if we do not find a diseased animal, we cannot be certain that the eradication attempt actually succeeded. The best we can do is to predict the probability of eradication success. Such modelling assumes that the more we search for the disease without finding it, the more confident we can be that we have succeeded.
There are now fewer than 90 cattle and deer herds infected with bovine tuberculosis (TB) in New Zealand, a drop of over 95% since 1994. Predicting the probability of TB eradication from particular areas enables limited resources to be allocated to areas where there is insufficient surveillance data and where success is less likely. Modelling TB freedom is complicated because of inherent sources of uncertainty, and the fact that the disease can be harboured by and transmitted between livestock (cattle and deer) and wildlife (possums). Here, Dean Anderson and his colleagues describe recent research aimed at modelling the combined probabilities of freedom of TB freedom for bothlivestock and wildlife, and how they account for uncertainty in the predictions generated.
Management decisions on whether to declare eradication success are based on predicted probabilities of freedom exceeding a specified threshold (e.g. > 0.95 probability of freedom). Standard probability calculations are used to combine the probabilities of freedom in livestock ‘AND’ wildlife, which results in a combined probability that is lower than the probabilities for the individual populations (Fig. 1). Consequently, predicted probabilities for both populations have to be well above the target threshold for the combined overall probability of freedom to surpass the threshold. Figure 1 illustrates how the individual population probabilities exceeded the threshold in 2008, but the combined probability did not reach the mark until 2009 (due to intensified surveillance).
The lines in Fig. 1 suggest that the team is certain about the predicted probabilities of freedom in livestock, wildlife and for the whole area. In reality, such probabilities are mean predictions from a model, and as such only represent a ‘best guess’. Consequently, sources of uncertainty are incorporated in the model. For example, field tests to detect TB in livestock are imperfect (e.g. the standard caudal-fold skin test used on cattle only has an 82% (95% CI = 74–90%) chance of detecting TB in an infected animal). Similar uncertainty exists in the tests used on wildlife, and also in the probability of disease transmission and capture. The level of uncertainty is indicated in the confidence intervals of the predicted probabilities of TB freedom.
Graphically representing the combined probability as a distribution (or histogram) allows Dean and his colleagues to assess this uncertainty. For example, two different surveillance scenarios could result in equal and satisfactory mean predicted probabilities of freedom (0.95), but very different levels of uncertainty (as measured by the 5th quantile; Fig. 2). Where there is high uncertainty, there is a high risk of being wrong in declaring the area disease-free. In contrast, where there is low uncertainty, or high confidence, the risk of being wrong in declaring eradication is relatively low. If managers are unsatisfied with the level of uncertainty associated with the predictions, additional surveillance will increase the accuracy and certainty in the model predictions.
Deciding how much extra disease management and/or surveillance is needed is always going to be difficult. The modelling described here can be used within a resource-allocation framework (see Nugent) to compute the amount of additional surveillance and/or wildlife control necessary to minimise the ‘net expected cost’ of being wrong (i.e. the joint cost in dollars of surveillance and renewed eradication operations). Minimising the cost of being wrong must include sources of uncertainty so that decisions are based on reliable model predictions.
Dean Anderson, Graham Nugent & Mandy Barron
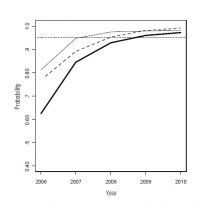
Fig. 1. Predicted mean probability of freedom from TB over time for livestock (thin line), wildlife (dashed line), and for both combined for the area (bold line). Only when the probability of freedom is sufficiently high (>95%) for both populations will the combined probability exceed the threshold (i.e. year = 2009).
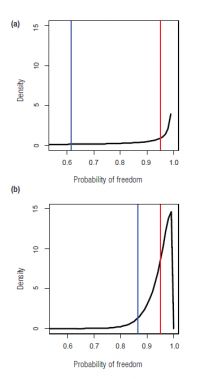
Fig. 2. Two different surveillance scenarios with predicted probability of TB freedom expressed as a distributions with means = 0.95 (red lines). (a) Scenario with high uncertainty in predictions as indicated by the low peak near the mean and low 5th quantile (0.62; blue line). (b) Scenario with low uncertainty in predictions as indicated by the high peak near the mean and relatively high 5th quantile (0.86; blue line).
